|
Introduction
IDADE2 uses observations of known-age skeletal specimens in a reference collection to estimate a relative likelihood distribution of ages at death for other observed specimens. The observations are described in up to twenty variables; each variable can be observed in up to 9 states, coded as integers 0 through 8, with 9 indicating a missing observation. The same variables and states used to observe and describe specimens in the reference collection must also be used to describe a specimen for whom age at death is to be estimated.
Methods
First, the reference collection is used to count frequencies: for each variable, the number of specimens in a given state and age class is counted. To determine age classes, a youngest age (ya) and age class width (acw) are chosen. In this series of age classes, age class 1 comprises specimens with age at death from ya to ya-1 + acw, and in general, age class 'a' comprises specimens with age at death from ya + (a-1)*acw to ya-1 + a*acw. For example, if ya = 15 and acw = 7, then age class 1 contains specimens with age at death from 15 to 21 years, age class 2 contains specimens with age at death from 22 to 28 years, etc. Among specimens in the reference collection, the number in each age class is also counted.
Theoretical considerations
Suppose a reference collection has been described for N variables. A specimen whose age at death is to be estimated would be described with a sequence of N states for those N variables observed for that specimen:
-
Let c1, c2, .., cN be such an observed sequence of states.
IDADE2 estimates the probability that the age at death of that specimen is in age class
'a' given that those states were observed.
-
Let C mean c1 and c2 and .. and cN were observed.
-
Let A mean the specimen is in age class 'a'.
- Bayes law:
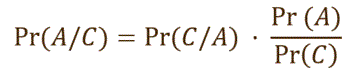
-
Assume variables are independent within an age class; then we have:
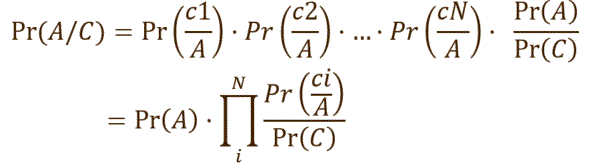
These theoretical results enable us to use observed frequencies to
estimate a predicted probability distribution over age classes for a
specimen with observed values for the N indicators.
Denote with the following notation:
- nfage[a] = number of reference specimens in age class 'a'
- nf = total number of reference specimens
- fre[i,a,ci] = number of reference specimens in age class 'a' and
in state ci for variable i
- Pr(A) is estimated by nfage[a] / nf
- Pr(ci/A) is estimated by fre[i,a,ci] / nfage[a]
These estimates are substituted in the equation above to begin to
calculate an estimated probability that the specimen is of age 'a'.
However, we do not have an explicit estimate for Pr(C). Although we
assume that within the narrow age classes the N variables are
independent, over the whole reference collection they must be
correlated with age (and thus with each other) if they are to be
useful as estimators of age. Thus, we cannot realistically assume
that the N variables are independent in order to estimate Pr(C).
Without further information, Pr(C) is basically unknown. However,
Pr(C), the probability of observing the sequence of states, is
unconditional (does not consider the age of the specimen), and so
we use it as a scaling factor chosen so to make the sum of the
probabilities of all the age classes equal 1. When Pr(C), estimated
in this way, is low, it suggest that the combination of states is
unusual in the context of the reference collection. If the scaling
constant is too small it calls into question the accuracy of the
estimate for two reasons: 1) it presses the limits of computational
accuracy of the computer, which could be improved (if warranted) by
using double precision calculations, which may not be warranted for
the next reason, and 2) a very small scaling constant is the result of the availability of only a few
specimens with the observed states for possible predicted ages. When the scaling constant falls below
0.0000001, there is so little data that IDADE does not attempt
to calculate a predicted age distribution.
For more information about input file formats of IDADE2 please visit the
help tab.
|









